Developing a Linear Regression Algorithm
Linear Regression is a Machine Learning model used to predict a continuous variable given one or more independent variables (features). When there is one continuous variable, we have a Single Variable Linear Regression. On the other hand, two or more independent variables is called a Multivariable Linear Regression.
While there are out-of-the box algorithms for Linear regression from libraries such as Scikit-Learn, in this post, I attempt to develop a Multivariable Linear Regression from scratch in order to understand the intuition behind such models.
LinearRegression models a linear relationship between one dependent and one or more independent variables. This is done by Parametric Learning.
Parametric learning entails finding the optimal parameter values that fits the linear relationship between variables.
The Linear Regression is specified as;
where $X_0 = 1$
and;
$(\theta_0, \theta_1, \theta_2,…, \theta_n)$ are the optimized thetas,
$(X_1, X_2,…, X_n)$ are the features or independent variables.
where our algorithm learns from our training data and outputs a prediction hypothesis $h_{(\theta)}(X)$ function which is used to predict actual values of $Y$.
where $\epsilon$ is the Error term.
The goal of parametric learning is to compute the optimal parameter values that fits the linear relationship between $Y$ and $X_i$ thereby minimizing $\epsilon$.
There are two ways to compute these optimized parameters;
- Gradient Descent
- Normal Equation
A general overview of the process;
- Import required libraries
- Develop model using both Gradient Descent and Normal Equation
- Test Model using both methods on a dataset and compare with Sklearn out-of-the box model using the Root Mean Square Error (RMSE)
RMSE is the average of the square differences between our hypothesis predicted values and the actual values.
It's used as a means to test for model accuracy.
Let’s import the important libraries:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
1. Gradient Descent
Optimization processes entail one of two things. Either maximize payoff or minimize cost.
Gradient Descent is a general process used to minimize several functions including the cost function. It works by
initializing the parameter values (with zero values), calculating the partial derivatives of cost function with respect to the parameters, subtracting a
scaled value of the partial derivative from the initial parameter until we arrive at the parameter values that makes cost function converge at a global minimum.
To compute optimized parameter values using Gradient Descent, we have to minimize the cost function. In statistics, there are several cost function but the one we'd use is the Squared Error Function which is specified as;
m = Number of Samples
def cost_function(X, y, init0s): #Returns the cost value given the theta values.
m = len(X) #m is the length of X i.e the number of samples
cost = 1/(2*m)*np.sum((np.dot(init0s, np.transpose(X)) - y)**2)
return cost
The goal is to Minimize $J_{(\theta)}$ to give optimized $\theta_j = (\theta_0, \theta_1, \theta_2,..., \theta_n)$ values.
To do this, we need the partial derivatives of the cosy function wrt each $\theta_j$ value.
$\alpha$ is the learning rate which specifies how big a step to take downshill when creating descent. IT must not be too large else the cost won't converge at minimum and it must not be too small else the the model take long to converge.
def partial_derivs(X, y, init0s): #Returns a list of updated thetas
m = len(X)
predicted = (np.transpose(init0s) * X).sum(axis = 1)
diff = (predicted - y)
diff_transpose = np.transpose(diff[:,np.newaxis])
#Add a new axis to make it vectorizable for dot product
updated0s = init0s - alpha*((1/m))* np.dot(diff_transpose, X)[0,:]
#Remove the extra dimension/axis
return updated0s
We need to keep calculating the partial derivatives of cost function with respect to the parameters, subtract a scaled value of the partial derivative from the initial parameter until we arrive at the parameter values that makes
cost function converge at a global minimum. Once the cost converges at minimum, the theta values will remain constant.
def gradient_descent(X, y,init0s):
#Returns the optimal theta value and a list of costs for each iteration
costs = [cost_function(X, y,init0s)]
for i in range(epochs):
init0s = partial_derivs(X, y,init0s)
c = cost_function(X, y, init0s)
costs.append(c)
return init0s, costs
def predict(X_test, y_test, optimal0s):
predicted = (np.transpose(optimal0s) * X_test).sum(axis = 1)
rmse = mean_squared_error(y_test, predicted)
return predicted, rmse
Let’s test out our Linear Regression model on a dataset
data = datasets.make_regression(100,2, noise = 1) #100 samples with two features
print(data)
(array([[ 0.0465673 , 0.80186103],
[-2.02220122, 0.31563495],
[-0.38405435, -0.3224172 ],
[-1.31228341, 0.35054598],
[-0.88762896, -0.19183555],
[-1.61577235, -0.03869551],
[-2.43483776, -0.31011677],
[ 2.10025514, 0.19091548],
[-0.50446586, -1.44411381],
...
[-2.06014071, 1.46210794],
[-0.63699565, 0.05080775],
[ 1.25286816, -0.75439794],
[ 1.04444209, 0.81095167],
[ 1.23616403, -1.85798186],
[ 2.18697965, 1.0388246 ],
[-0.07557171, 0.48851815],
[ 0.59357852, 0.40349164]]), array([ 72.36523412, -37.14156866, -41.38412368, -12.64791154,
-43.66708325, -55.37682786, -104.14429178, 86.72486169,
-141.78457722, -57.09382215, 21.11295519, 37.8001059 ,
199.5500905 , 25.81364514, 209.42911479, 128.20604958,
-26.3460515 , -88.2946975 , 45.84342752, -29.55352689,
...
102.81595456, -28.66364244, 100.21268739, -73.03008828,
113.01648102, 109.17545836, -31.30447011, 36.51499677,
-88.82089559, -3.4467088 , 53.45209032, -87.40808263,
-99.40016109, 5.04506704, 56.12030581, 84.54855562,
59.02884225, -17.38215753, -24.1274554 , 102.33610869,
-120.59599797, 160.11974736, 39.67236875, 55.97220222]))
We need to carry out some preprocessing on data.
- Add the $X_0$ column with 1’s
- Split the data into Train and Split for Validation
def preprocess_data(data):
X = data[0]
y = data[1]
#copy = data.copy
ones = np.ones(len(X))
X = np.c_[ones, X]
return train_test_split(X, y, test_size=0.33, random_state=1)
X_train, X_test, y_train, y_test = preprocess_data(data)
#y_train
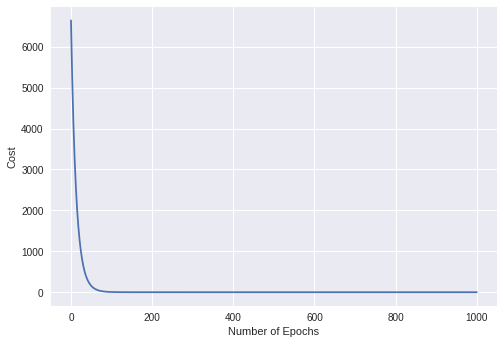
Plot the Cost values
To check that our gradient descent theta values are actually optimized, we have to plot the cost values to check for convergence
epochs = 1000 #Number of Iterations
alpha = 0.04
init0s = np.zeros(3)
y = gradient_descent(X_train, y_train, init0s)[1]
x = np.arange(len(y))
plt.xlabel("Number of Epochs")
plt.ylabel("Cost")
plt.plot(x,y)
[<matplotlib.lines.Line2D at 0x7f2d50903ac8>]
The cost values fall for each 100 iterations until it converges at a value close to zero.
Optimal Theta Values
gradient_descent(X_train, y_train, init0s)[0]
array([ 0.19357013, 32.19125678, 86.08455637])
So our multivariable linear regression prediction model is;
$h_{(\theta)}(X)$ = 0.19357013$X_0$ + 32.19125678$X_1$ + 86.08455637$X_2$
Compare our model’s RMSE with Sklearn’s
epochs = 1000 #Number of Iterations
alpha = 0.04
init0s = np.zeros(3)
predict(X_test, y_test, gradient_descent(X_train, y_train, init0s)[0])[1]
#Returns the model RMSE
1.4033255546659869
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
prediction = lr.predict(X_test)
rmse = mean_squared_error(y_test, prediction)
rmse
1.4033255545376973
Our model’s RMSE value (1.40332) is comparable to Sklearn’s RMSE value (1.40332)
2. Normal Equation
The normal equation uses linear algebra to compute the optimal theta values at once.
where $\theta_j = (X^TX)^{-1}X^TY$
The normal equation is useful when number of features is not very large and $(X^TX)$ is invertible. Otherwise, Gradient Descent should be used. With Normal Equation, there is no iteration or initializing of theta values.
def normal_equation(X, y):
xtrans = np.transpose(X)
inv = np.linalg.pinv(np.dot(xtrans, X))
#use pinv for nonivertible singular matrices and use inv for normal invertible matrices
optimal0s = np.dot(np.dot(inv, xtrans), y)
return optimal0s
normal_equation(X_train, y_train)
array([ 0.19357013, 32.19125678, 86.08455637])
We can see that the values for the normal equation are similar to that of gradient descent.
