Regularized Multiclass Logistic Regression Algorithm
Logistic Regression is a Classification Machine Learning model used to predict a discrete variable given one or more independent variables. Classification entails assigning a class to each sample based on the learned parameters.
A real life example is;
Given a symmetrical college classroom where each student seated in the room is identified by a row and column value, we can develop a logistic regression model to classify whether each student is male or female. This type of classification is called Binary Classification. i.e
$$Y \in 0,1 $$
Alternatively, if the class room contains first year, second year, third-year, and fourth year student, we can classify whether each student is year 1, 2, 3, or 4. This type is called Multi-class Logistic Regression. i.e
$$Y \in 1,2,3,4 $$
While there are out-of-the box algorithms for Logistic regression from libraries such as Scikit-Learn, in this post, I'd develop a Multivariable Logistic Regression model (that will also work for Binary Classification) from scratch in order to understand the intuition behind such models.
The Logistic Regression is specified as;
where $X_0 = 1$
We can see that $g(X)$ is similar to a Linear Regression. But our Logistic regression model must output probability values between 0 and 1 which specify probaility of each sample belonging to each class. To do this, we pass the $g(X)$ into a Sigmoid function $g(z)$;
For a binary classification, $h_{(\theta)}(X)$ will output the probability that the sample instance is in Class 1. We state a decision boundary that says that if this probability value is $>0.5$, sample is in class 1. Else if the probability value is $<0.5$, sample is in Class 0.
This same method is applied in Multi class classification using the One-vs-All. For example, given a data with 4 classes, we'd train 4 different binary classification model, where for each model one class is assigned 1 and the others are assigned 0. At the end of the iteration, each sample instance will output an array of probability values that sum to 1, stating the probability of each sample instance belonging to class 1, 2, 3, and 4 so that the class with the highest probability is predicted.
A key aspect of logistic regression is defining the decision boundary. The decision boundary is delineated by;
Without properly defining the decision boundary, our sigmoid function will output probability values that do not properly classify our sample instances.
Gradient Descent is used to arrive at the optimal parameters $\theta_j = (\theta_0, \theta_1, \theta_2,..., \theta_n)$ values which fits our data. Gradient descent works by initializing the parameter values (with zero values), calculate the partial derivative of cost function with respect to the parameters, subtract a scaled value of the partial derivative from the initial parameter until we arrive at the parameter values that makes cost function converge at a global minimum.
A general overview of the process
- Import required libraries
- Develop model using both Gradient Descent
- Test Model using both methods on a dataset and compare with Sklearn out-of-the box model using prediction accuracy
Lets import the important libraries:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
We need a cost function that gives a cost of zero if our model $h_{(\theta)}(X)$
prediction equals $Y$ and gives a cost that ranges to infinity if our model $h_{(\theta)}(X)$ prediction is unequal to the actual $Y$ value.
A problem that may arise with logistic regression is overfitting. This is when our logistic model predicts well on the training dataset but is unable to perform well on previously unseen data. This result when there are many features. With regularization, our goal here is to determine the best decision boundary and also avoid overfitting. To do this we'll add a regularization parameter that helps to control the tradeoff between our two different goals.
Such cost function is stated as;
m = Number of Samples
n = Number of features
def logistic_cost(X_train, y_train, init0s):
#Returns the cost of our Logistic Regression model given a set of theta parameters (init0s)
m = len(X_train)
product = (np.transpose(init0s) * X_train).sum(axis = 1)
#print(product)
sigmoid = 1 / (1+ (np.exp(-product)))
a = (y_train * np.log(sigmoid))
b = ((1 - y_train) * np.log(1 - sigmoid))
c = (lambdaa/2*m)*((init0s[1:]**2).sum())
cost = (-1/m)*np.sum(a+b) + c
return cost
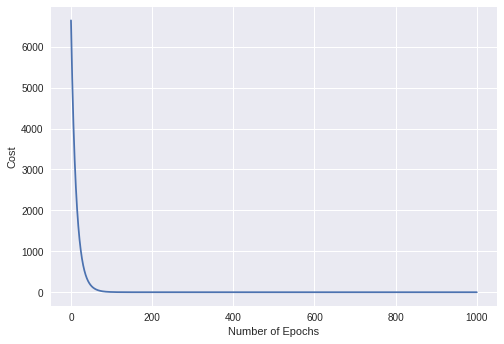
The goal is to Minimize $J_{(\theta)}$ to output optimized $\theta_j = (\theta_0,\theta_1, \theta_2,…, \theta_n)$ values.
To do this, we need the partial derivatives of the cost function with respect to each $\theta_j$ value.
Note that the second part of our cost function sums from i = 1 to n. So we'll have a different equation for $\theta_0$ and $(\theta_1, \theta_2,..., \theta_n)$
def partial(X_train, y_train, init0s):
#Returns the partial derivate of the cost function with respect to each theta value
m = len(X_train)
prod = (X_train * init0s).sum(axis = 1)
sigmoid = 1 / (1+ (np.exp(-prod)))
diff = (sigmoid - y_train)
update0 = np.asarray(init0s[0] - (alpha/m)*np.dot(diff.transpose(), X_train[:,0]))
updatej = init0s[1:]*(1 - alpha*(lambdaa/m)) - (alpha/m)*np.dot(diff.transpose(), X_train[:,1:])
return np.concatenate([np.expand_dims(update0, axis=0), updatej], axis = 0)
We need to keep calculating the partial derivatives of cost function with respect to the parameters, subtract a scaled value of the partial derivative from the initial parameter until we arrive at the parameter values that makes cost function converge at a global minimum. Once the cost converges at minimum, the theta values will remain constant.
def gradient_descent(X_train, y_train, init0s):
#Returns the optimal theta value using 3000 iterations
for i in range(3000):
init0s = partial(X_train, y_train,init0s)
return init0s
To implement One-vs-All classification, we have to iterate over each class and replace with 1's and 0's.
1 for the chosen class and 0 for others
def oneVsAll(y_array, class_val):
#Seperates Y into 1's and 0's for each chosen class
for i in range(len(y_array)):
if y_array[i] == class_val:
y_array[i] = 1
elif y_array[i] != class_val:
y_array[i] = 0
return y_array
def multiClassThetas(X_train, y_train, init0s):
#Returns a matrix of the optimal theta values with dimension k * n
#where k is the number of classes and n is number of features
y_copy = y_train.copy()
thetas_list = []
for i in np.unique(y_train):
copy = y_train.copy()
y_copy = oneVsAll(copy, i) #Seperate target into 0s and 1s
class_thetas = gradient_descent(X_train, y_copy, init0s)
thetas_list.append(class_thetas)
all_thetas = np.c_[thetas_list]
return all_thetas
def p_values(thetas, X_train, y_train):
#Returns each sample instances' probability values for each class with dimension k * m
#Where k is the number of classes and m is number of samples
x_tranpose = X_train.transpose()
p_values = []
for theta in thetas:
dot_product = np.dot(theta, x_tranpose)
p_values.append(1 / (1+ (np.exp(-dot_product))))
return np.c_[p_values]
def predict(p_values):
#Returns predictions
prediction = np.argmax(p_values, axis = 0)
return prediction
def accuracy_score(prediction, actual):
#Returns accuracy score (%)
accuracy_score = sum(prediction == actual) / len(actual)
return accuracy_score
Let’s test our model on a dataset
Our dataset is copy of the test set of the UCI ML hand-written digits datasets containing 8x8 images of integer pixels in the range 0 - 16. The integers range from 0 - 9
digits = datasets.load_digits()
digits
{'DESCR': "Optical Recognition of Handwritten Digits Data...
'data': array([[ 0., 0., 5., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.],
[ 0., 0., 0., ..., 16., 9., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 2., ..., 12., 0., 0.],
[ 0., 0., 10., ..., 12., 1., 0.]]),
'images': array([[[ 0., 0., 5., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 15., 5., 0.],
[ 0., 3., 15., ..., 11., 8., 0.],
...,
[ 0., 4., 11., ..., 12., 7., 0.],
[ 0., 2., 14., ..., 12., 0., 0.],
[ 0., 0., 6., ..., 0., 0., 0.]],
[[ 0., 0., 0., ..., 5., 0., 0.],
[ 0., 0., 0., ..., 9., 0., 0.],
[ 0., 0., 3., ..., 6., 0., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.]],
[[ 0., 0., 2., ..., 0., 0., 0.],
[ 0., 0., 14., ..., 15., 1., 0.],
[ 0., 4., 16., ..., 16., 7., 0.],
...,
[ 0., 0., 0., ..., 16., 2., 0.],
[ 0., 0., 4., ..., 16., 2., 0.],
[ 0., 0., 5., ..., 12., 0., 0.]],
[[ 0., 0., 10., ..., 1., 0., 0.],
[ 0., 2., 16., ..., 1., 0., 0.],
[ 0., 0., 15., ..., 15., 0., 0.],
...,
[ 0., 4., 16., ..., 16., 6., 0.],
[ 0., 8., 16., ..., 16., 8., 0.],
[ 0., 1., 8., ..., 12., 1., 0.]]]),
'target': array([0, 1, 2, ..., 8, 9, 8]),
'target_names': array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])}
Let’s preview some of the images
#Preview 12 random digits
X = digits["images"]
y = digits["target"]
import random
images_labels = list(zip(X, y))
plt.figure(figsize = (10,10))
for index, (image, label) in enumerate(random.sample(images_labels, 12)):
plt.subplot(3, 4, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title('Data Label: %i' % label)
We need to carry out some preprocessing on data.
- Add the $X_0$ column with 1’s
- Split the data into Train and Split for Validation
- To apply classification on the images, we need to flatten each image, to turn the data into a (n_samples, feature) matrix
print(digits["images"].shape)
n_samples = len(digits["images"])
data = digits["images"].reshape((n_samples, -1))
print(data.shape)
(1797, 8, 8)
(1797, 64)
def preprocess_data(data,y):
ones = np.ones(len(data))
X = np.c_[ones, data]
return train_test_split(X, y, test_size=0.33, random_state=1)
X_train, X_test, y_train, y_test = preprocess_data(data,y)
X_train.shape
(1203, 65)
Define our parameters
k = set(y_train)
n = X_train.shape[1]
alpha = 0.04
lambdaa = 0.05
init0s = np.zeros(n)
Compute Matrix of Optimal Theta Values
multiClassThetas(X_train, y_train, init0s)
array([[-1.31403414e-02, 0.00000000e+00, -2.59377216e-02,
-6.31274886e-02, 1.17253991e-02, -6.06195972e-02,
-2.76216506e-01, -9.60726849e-02, -5.54443559e-03,
-8.48525208e-05, -1.00972740e-01, 2.88416771e-02,
1.04467197e-01, 1.07517451e-01, 1.61677709e-01,
-3.71528350e-02, -6.06298079e-03, -3.37027101e-05,
5.51556629e-03, 9.99805984e-02, -1.08265132e-02,
-3.00130630e-01, 2.04669085e-01, -2.50503394e-02,
-5.75540152e-03, 0.00000000e+00, 5.90709193e-02,
2.60611419e-02, -1.65867238e-01, -5.10127664e-01,
3.67345821e-02, 1.94052814e-02, -2.13619661e-03,
0.00000000e+00, 1.29252327e-01, 1.19501559e-01,
-2.04148052e-01, -4.83251015e-01, -9.39189012e-02,
5.43727903e-02, 0.00000000e+00, -4.59732987e-03,
-9.73487551e-03, 2.18226777e-01, -1.83718565e-01,
-4.36895134e-01, -2.98278190e-02, 4.10059111e-02,
-6.33254170e-04, -1.70621937e-02, -7.48627421e-02,
7.73939584e-02, -7.36453344e-02, 1.00845110e-01,
1.66573583e-02, -1.53046258e-01, -2.86943181e-02,
-1.72545249e-05, -2.68832033e-02, -1.40561491e-01,
1.99166050e-02, -1.11080662e-01, -8.32626265e-02,
-1.17986780e-01, -2.64299665e-02],
[-2.69920699e-01, 0.00000000e+00, -1.04710063e-01,
3.40595678e-01, 3.12234356e-02, -5.64479044e-01,
3.47876069e-01, 1.12295951e-02, -9.31376715e-02,
-6.28977921e-04, -6.39244863e-01, -6.02478561e-01,
-3.31540223e-01, 1.37080523e-02, 2.20134008e-01,
-3.68506113e-01, -6.10117031e-02, -2.08931048e-04,
5.06888290e-01, 1.49183942e-01, 4.48823730e-01,
3.14246111e-01, -3.91285806e-01, 2.12113023e-01,
-6.55962009e-03, 0.00000000e+00, -2.74605434e-01,
3.75841347e-02, 1.42843851e-01, -1.04040246e-02,
9.69674873e-02, -2.23627666e-01, -9.41148407e-05,
0.00000000e+00, 1.37636303e-02, -9.77820381e-03,
-3.65732736e-01, 2.80348134e-01, -9.46361310e-02,
-3.88469464e-01, 0.00000000e+00, -1.94733356e-03,
-6.18295375e-01, 5.00341696e-02, 1.19085853e-01,
-9.93209820e-02, -1.65864730e-01, -2.53260827e-01,
-5.71349313e-03, -1.12283576e-02, -2.59447562e-01,
-4.69374156e-02, 1.37028882e-01, 9.03339949e-02,
-1.02199302e-01, -2.68638669e-01, 3.93152618e-01,
-3.60629707e-03, -2.03306602e-01, -3.15610518e-01,
-1.29422171e-02, 7.87461417e-02, 1.87173583e-01,
-2.86360508e-01, 2.73121918e-01],
...
Compute Probability values using optimal thetas on the Test set
optimal_thetas = multiClassThetas(X_train, y_train, init0s)
p_values(optimal_thetas, X_test, y_test)
array([[1.30693813e-10, 5.47023277e-05, 9.99988296e-01, ...,
5.69104368e-12, 2.71614471e-09, 9.99978225e-01],
[9.50544243e-01, 6.62287815e-08, 2.03516481e-10, ...,
5.34710312e-11, 2.22894272e-04, 9.88195491e-08],
[1.71002761e-06, 2.92223351e-05, 3.23123282e-06, ...,
7.73583827e-06, 7.06966327e-16, 4.44882769e-06],
...,
[1.67917238e-06, 6.32334394e-02, 2.18410678e-07, ...,
1.03953150e-06, 2.22179681e-06, 8.15802069e-07],
[4.96943926e-03, 3.67007637e-05, 4.79761046e-11, ...,
6.25440616e-01, 3.62788141e-07, 1.79991157e-07],
[4.16670602e-07, 3.59481313e-05, 6.75722211e-08, ...,
1.77055305e-06, 3.09914373e-05, 1.89162455e-07]])
Compute Test Predictions
prob = p_values(optimal_thetas, X_test, y_test)
predict(prob, y_test)
array([1, 5, 0, 7, 1, 0, 6, 1, 5, 4, 9, 2, 7, 8, 4, 6, 9, 3, 7, 4, 7, 4,
8, 6, 0, 9, 6, 1, 3, 7, 5, 9, 8, 3, 2, 8, 8, 1, 1, 0, 7, 9, 0, 0,
8, 7, 2, 7, 4, 3, 4, 3, 4, 0, 4, 7, 0, 5, 9, 5, 2, 1, 7, 0, 5, 1,
8, 3, 3, 4, 0, 3, 7, 4, 3, 4, 2, 9, 7, 3, 2, 5, 3, 4, 1, 5, 5, 2,
5, 2, 2, 2, 2, 7, 0, 8, 1, 7, 4, 2, 3, 8, 2, 3, 3, 0, 2, 9, 5, 2,
3, 2, 8, 1, 1, 9, 1, 2, 0, 4, 8, 5, 4, 4, 7, 6, 7, 6, 6, 1, 7, 5,
6, 3, 8, 3, 7, 1, 8, 5, 3, 4, 7, 8, 5, 0, 6, 0, 6, 3, 7, 6, 5, 6,
2, 2, 2, 3, 0, 7, 6, 5, 6, 4, 1, 0, 6, 0, 6, 4, 0, 9, 3, 5, 1, 2,
3, 1, 9, 0, 7, 6, 2, 9, 3, 5, 3, 4, 6, 3, 3, 7, 4, 8, 2, 7, 6, 1,
6, 8, 4, 0, 3, 1, 0, 9, 9, 9, 4, 1, 8, 6, 8, 0, 9, 5, 9, 8, 2, 3,
5, 3, 0, 8, 7, 4, 0, 3, 3, 3, 6, 3, 3, 2, 9, 1, 6, 9, 0, 4, 2, 2,
7, 9, 1, 6, 7, 6, 5, 9, 1, 9, 3, 4, 0, 6, 4, 8, 5, 3, 6, 3, 1, 4,
0, 4, 4, 8, 7, 9, 1, 5, 2, 7, 0, 9, 0, 4, 4, 0, 1, 4, 6, 4, 2, 8,
5, 0, 2, 6, 0, 1, 8, 2, 0, 9, 5, 6, 2, 0, 5, 0, 9, 1, 4, 7, 1, 7,
0, 6, 6, 8, 0, 2, 2, 6, 9, 9, 7, 5, 1, 7, 6, 4, 6, 1, 9, 4, 7, 1,
3, 7, 8, 1, 6, 9, 8, 3, 2, 4, 8, 7, 5, 5, 6, 9, 9, 9, 5, 0, 0, 4,
9, 3, 0, 4, 9, 4, 2, 5, 4, 9, 6, 4, 2, 6, 0, 0, 5, 6, 7, 1, 9, 2,
5, 1, 5, 9, 8, 7, 7, 0, 6, 9, 3, 1, 9, 3, 9, 8, 7, 0, 2, 3, 9, 9,
2, 8, 1, 9, 8, 3, 0, 0, 7, 3, 8, 7, 9, 9, 7, 1, 0, 4, 5, 4, 1, 7,
3, 6, 5, 4, 9, 0, 5, 9, 1, 4, 5, 0, 4, 3, 4, 2, 3, 9, 0, 8, 7, 8,
6, 9, 4, 5, 7, 8, 3, 7, 8, 3, 2, 6, 6, 7, 1, 0, 8, 4, 8, 9, 5, 4,
8, 2, 5, 3, 3, 3, 5, 1, 8, 7, 6, 2, 3, 6, 2, 5, 2, 6, 4, 5, 4, 4,
9, 7, 9, 1, 0, 2, 6, 9, 3, 6, 7, 3, 6, 4, 7, 8, 4, 1, 2, 1, 1, 0,
7, 3, 0, 3, 2, 9, 4, 5, 9, 9, 4, 8, 3, 3, 3, 8, 4, 1, 4, 5, 8, 3,
9, 5, 4, 7, 7, 4, 0, 1, 7, 9, 8, 0, 9, 6, 0, 9, 8, 6, 3, 1, 4, 6,
5, 1, 9, 0, 1, 5, 2, 5, 0, 2, 5, 4, 7, 2, 2, 3, 2, 1, 8, 4, 9, 6,
3, 7, 1, 1, 1, 8, 8, 8, 8, 5, 9, 1, 7, 1, 2, 7, 9, 7, 4, 3, 4, 0])
Check for Accuracy
prediction = predict(prob)
accuracy_score(prediction, y_test)
0.9696969696969697
Compare With Sklearn’s Logistic Regression Module
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X_train, y_train)
accuracy_score(y_test, lr.predict(X_test))
0.9562289562289562
Our model’s accuracy score on the Test set is 96.96% which is better than Sklearn’s 95.6%
Let’s check the performance of our model visually. To do this, we have to remove the $X_0$ (1) values and reshape to shape (n_samples, 8, 8)
X_test_reshaped = X_test[:,1:].reshape(len(X_test), 8, 8)
X_test_reshaped.shape
(594, 8, 8)
images_prediction = list(zip(X_test_reshaped, prediction))
plt.figure(figsize = (10,10))
for index, (image, prediction) in enumerate(random.sample(images_labels, 12)):
plt.subplot(3, 4, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title('Predicted: %i' % prediction)
